This talk was given by videoconference at the 50 Years of Public Computing at the University of Illinois conference at Urbana-Champaign on Thursday, April 15, 2010

Thank you very much.

Well, I’m pleased to be here today, even if in virtual form.

You know, in a month it’ll be exactly a year since we were two miles away from where you are right now… doing this.

It was quite tense.

The culmination of about 5 years of work, and 25 more years of previous development.

We were going to launch Wolfram|Alpha.

An absurdly ambitious project that I hadn’t been sure was going to be possible at all.

Our long-term goal was—and is—to make all the world’s systematic knowledge computable.

To take all the data, and models, and methods that our civilization has accumulated—and set it up so that it can immediately be used to compute answers to whatever questions people ask.

There’s a long, long history to this basic idea.

Leibniz was talking about a version of it 300 years ago.

And 50 years ago, when computers were young, it seemed like it wouldn’t be long before it was possible.

But people mostly thought that it’d happen by computers managing to emulate brains—and pulling in knowledge and processing like we humans do.

Well, I myself am right now 50 years old… and, as perhaps I’ll show you later, I’d actually been thinking about globally systematizing knowledge since I was a kid.

It was about 30 years ago when I first started thinking about making knowledge broadly computable.

And at the time I concluded it’d require solving the whole problem of artificial intelligence—and was way out of reach.

But then I spent the next 25 years doing things that, as I’ll explain, finally made me think: maybe, just maybe, this computable knowledge idea isn’t so out of reach.

I must say that at first I still didn’t know if it was only not out of reach in the 50-year-type time frame. Or the 20-year. Or the 5-year.

But I decided that we should give it a try.

And 11 months ago today all the work we’d put in was concentrated in this control room about 2 miles from here.

It had all started with some abstract intellectual ideas.

And now, in the end, it had turned into millions of lines of code, terabytes of data—and 10,000 servers that we’d just been finishing assembling.

Some news had come out about our project.

So there was a lot of anticipation.

And we knew there’d be a big spike in people wanting to try out what we’d done.

We’d obviously done lots of testing. But we really didn’t have any idea what would happen when millions of people actually started accessing our system.

But we thought: let’s let as many people as possible share the experience of finding out.

So we decided to do a live webcast of the moment when we actually made our system live to the world.

Well, actually, the day of the event I was thinking: this is going to be such boring TV.

All that’s going to happen is that at some moment we’ll push a virtual button, and everything will go live.

Well, needless to say, it didn’t stay boring long.

Early in the day, we had finally finished assembling all our servers—and were able to switch them all on.

And… oh my gosh… lots of stuff didn’t work.

Well, at the appointed time we started the live webcast.

And still things weren’t working.

There was a horrible networking and load balancing problem.

We’d advertised 9pm as our go-live time.

We figured at that time on Friday evening most people wouldn’t be thinking about us… so we’d have a comparatively soft launch.

Well, with perhaps 15 minutes to go, we’d finally solved the main technical problem.

You know, some people had said when you look at other peoples’ control rooms they often have television weather and news playing. Perhaps we should have that too.

I said bah, we won’t need that. This is just a computer thing. We don’t care if it’s raining.

Well, fortunately we did actually have good weather and news feeds.

Because this was May in the Midwest.

And as it turned out, with perhaps 30 minutes to go, there was another problem.

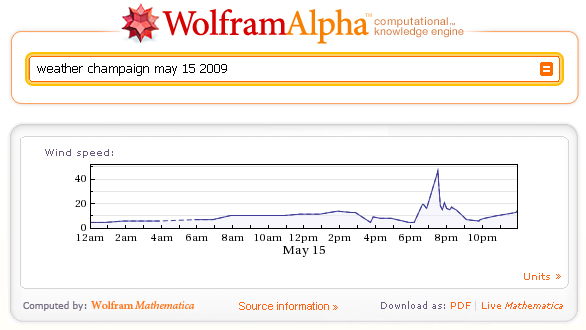
Here, we can actually look at live Wolfram|Alpha to find out about it.

See that giant spike in wind speed just before 8pm?

That was a tornado. Approaching our location.

Well, we had backup generators—and of course we had several remote colocation sites for our servers.

But still, we had a tornado coming straight for us.

Well, fortunately, at the last minute, it turned away.

And the power didn’t even go out.

So at 9:33:50pm central time on May 15, 2009, I pressed the button, and Wolfram|Alpha went live.

And our giant project was launched—out of the starting gate.

Well, I thought I would talk a little bit here about the background to how we got there.

And how it was, for example, that we were two miles away from here, in Champaign, Illinois.

The story goes a long way back.

I was a kid, growing up in England in the 1960s.

At first, I had really been into the space program.

But by the time I was 10 or 11, I had decided that actually physics was where it was really at.

So I started teaching myself physics, and pretty quickly started reading college physics books and so on.

Well, in the summer of 1972, when I was 12 years old, I happened to get this book.

And I got really interested in the foundations of thermodynamics and statistical physics—and in reproducing the process on the cover.

Well, it so happened that I was about to get my hands for the first time on a computer.

A teacher at the high school I went to—a school called Eton—had been a friend of Alan Turing’s.

And through that he had gotten connected to computers. And somehow a decade and a half later he’d managed to get the school given a computer.

A thing called an Elliott 903C.

About the size of a large desk. With 8K of 18-bit words of core memory.

And programmed with paper tape.

Well, I started programming that machine.

My top goal was to reproduce this physics process.

And in the process, I learned quite a bit about programming.

I think probably my finest achievement was a paper tape loader for which I had to invent some kind of error-correcting code.

And for my physics simulation, I actually invented something neat too—I invented a simple kind of computational system that, although I didn’t know it at the time, is called a cellular automaton.

Well, a decade later I made lots of interesting discoveries using cellular automata.

But back in 1973, as luck would have it, the particular cellular automaton I investigated just managed to avoid any of the interesting phenomena I saw later.

I sometimes wonder whether I would actually have recognized those phenomena for what they were back in 1973.

But in any case, I went on to other problems—and in particular got very deeply involved in particle physics, and quantum field theory.

Well, one feature of those areas is that they’re full of very, very complicated algebraic calculations.

Which I have to say I as a human wasn’t very good at.

And it might have been a disqualifying handicap.

But what I realized was that actually I didn’t need to do all this algebra; I could just get a computer to do it.

And in 1976 I started ramping up to eventually become probably the world’s largest user of the various algebraic computing systems that had been developed at that time.

It was fun. I would write a paper where I would say, “From this one can calculate…” and then give some incredibly complicated formula.

I could always tell when people were reading my papers, because I’d get these questions: “How did you derive formula number such-and-such?” “You must be so good at doing algebra.”

“No,” I said, “I just got a computer to do it.”

I’m not sure in those days people really believed me.

But anyway, by 1979 I had pretty much outgrown all the systems that had been developed so far.

And so… a few months after my 20^th birthday, and a couple of weeks after I had gotten my physics PhD at Caltech, I decided that my best option was just to build my own computational system.

I remember going to the Caltech bookstore and buying all the available books on computer science at the time. And over the course of a few weeks, systematically going through them.

I wanted to make a very general system.

So I kind of operated a bit like a physicist—thinking about different kinds of computations I thought I might someday want to do.

And trying to figure out what underlying building blocks—what primitives—they were built from.

What I came up with is what I’d now call symbolic programming.

And I assembled a team, and started implementing the system—in what was then the newfangled language C.

Well, almost exactly 30 years ago today the system first came alive.

What I called SMP—the “symbolic manipulation program”—was born.

I realized of course that the system wasn’t just useful to me, but potentially to lots of other people—at least if they had access to the one of the big minicomputers of the time.

And in 1981 the system was to the point where it could really be released.

I was by then a young faculty member in physics at Caltech.

I didn’t really know anything about business. But I eventually backed into the realization that the only way to really give the system its best chance was to start a company to develop it.

Well, in those days universities were pretty confused about spinoff companies, and I got caught in the middle of some pretty spectacular confusion.

But the company did get started.

A side effect was that I quit my job at Caltech, and moved to the Institute for Advanced Study in Princeton.

Which had the interesting feature that in von Neumann’s time, it had effectively “given away” the computer, so it felt OK about not trying to own technology that people developed there.

Well, particularly during the time of confusion with Caltech, I’d decided what the heck, let me do a project that’s just fun.

At first, I thought about trying to do something related to—sort of extending my SMP project—and trying to make a computer system that would do brain-like things.

But somehow that morphed into a version of my pre-teen interest: of trying to understand how it is that complex things can happen anywhere in the universe, in brains or cosmology.

Well, at first I thought about all sorts of complicated models for that.

But then I decided to just start simple. I think it was the experience I’d had in developing SMP.

I kind of wondered: just like I can make primitives for a computer language, can I make primitives for how nature works?

So I started looking at the very simplest possible programs.

Not like typical computer programs we write. Those are complicated things that we construct for particular purposes.

More like “naturally occurring programs”. Really simple ones that might sort of arise at random.

Well, here was the big experiment I did.

In line-printer-output form from 1982.

And in modern Mathematica form.

And the big point here is that although many of these simple cellular automaton programs just do very simple things, there are these amazing examples where one just starts from a simple seed, follows a simple rule, and gets all this amazing stuff.

Suffice it to say that this picture is I think the single most surprising discovery I’ve ever made.

I had had the intuition—which one gets from engineering and so on—that to make something complicated, one had to use complicated rules and go to lots of effort.

But here was an example where just a really simple rule could produce all sorts of complexity.

Well, in nature we see lots of complexity.

And the exciting thing was that this example seemed like it finally showed the secret that nature uses to make that complexity.

Just by sort of sampling programs out there in the computational universe of possible simple programs.

Well, I thought this was pretty exciting.

And that this whole idea of simple rules producing complex behavior should lead to a very interesting new area of science.

Well, I did lots of work in this direction myself.

And I pulled in quite a few other people as well.

But I thought that what was really needed was a whole army to really start conquering this area of science.

Well, by this point—partly as a result of starting the company around SMP—I’d begun to think that I wasn’t completely hopeless as an organizer of things.

So I decided I should try to launch this area of science—which I called “complex systems research”.

So I wrote up manifestos for the science, and went around telling people what a good idea the science was.

I started a journal for the science—which was actually the very first fully computer-produced journal in any area—and that in fact I still publish today, 25 years later.

And I wanted to start some kind of institute for the science too.

I was pretty businesslike about it. I wrote up a plan, and went around effectively getting bids from a bunch of universities.

Well, so, as you might guess, what happened was that the University of Illinois won.

So with the lead taken by the Physics Department, and with support from NCSA, and connections to the Computer Science and Math Departments—in the fall of 1986, I came to Illinois to start the Center for Complex Systems Research.

I’m happy to say that the University of Illinois did well in living up to its promises.

CCSR got off to a good start. And I think we recruited quite a lot of interesting people to Illinois.

But one bug I realized is that when you have a new direction in science, there aren’t really right off the bat many professor-level people who do it.

So it was hard really to fully staff up.

And I must admit that I realized that at age 27 I wasn’t completely cut out to be a university administrator.

So in the fall of 1986, very soon after I’d actually come to Illinois, I started thinking about other ways to move my science and my objectives forward.

I was a bit impatient with the general development of complex systems theory—or complexity theory, as it later was more often called.

CCSR at Illinois was the very first complexity institute. Today there are hundreds of complexity institutes.

But back in 1986 it seemed like it would take forever for all the funding and organizational structure to build up. And what was building up, I thought was too mushy, and not really pursuing the interesting basic science.

Well, so my first idea had been to get lots of other people into doing science I think is good.

But soon after arriving in Illinois, I hatched a Plan B: build the absolutely best tools I can, and put myself in the best personal situation I can, then try to push forward on the science myself as fast as possible.

Well, by that time the SMP company had wandered off in other directions, and I had largely detached from it. In the mid-1990s, after many adventures, it actually went public, only to be gobbled up by a series of bigger fishes.

But so I decided I need to build a new, more general, computational system.

And that I needed to start and run a company to do that.

And that was how Mathematica—and Wolfram Research—got started.

Right here in Champaign, Illinois.

At first, of course, it was a tiny operation.

But in an amazingly short time—basically only 18 months—we got to the point of having a first version of Mathematica.

And through other things I had done I was by then quite connected into the computer industry, and so we were able to start making various deals and things.

And on June 23, 1988, in Santa Clara, California, we officially released Version 1.0 of Mathematica.

And very quickly we started to grow our company in Champaign.

By 1991, we were developing a substantial and broadening customer base, and we were able to release Version 2 of Mathematica.

It was great to see our R&D and our company growing so well.

But I think perhaps what I was most excited about was that I had a really great tool to use myself.

So in mid-1991, just after the release of Mathematica 2, I decided that I would go away for a little while, and push forward on the science I had been doing.

I used technology to become a remote CEO, first in California, then in Chicago, and later in Boston.

And meanwhile I was using Mathematica to discover some really incredible things.

And the “year or so” that I had expected to spend doing that stretched into nearly 11 years.

But finally in 2002, I finished wrapping up all the science that I had figured out into a big book.

NKS—as the field that’s based on the book is usually called—has a lot of important implications in science, in ways of thinking about things, and in technology.

Well, in the time I’d been writing the book, we’d built up a terrific team at Wolfram Research, and lots and lots of things had been achieved.

We’d been pouring algorithms and capabilities into Mathematica.

But more importantly, we’d slowly been realizing that the fundamental ideas of Mathematica were capable of supporting vastly more.

It’s funny really. One builds some kind of paradigm. Then one lives in it for perhaps a decade. And then one starts to understand what its real significance is.

Well, that’s the way it was with Mathematica.

We had the idea of having this really unified system, built on the principle that anything could be represented as a symbolic expression.

At first we knew that algorithmic, formal kinds of things could be represented that way. Mathematical kinds of things. Things about data. Things about geometry or graphics.

And we knew that all these things could be manipulated in a very uniform way by the operations in our unified symbolic language.

Well, by the mid-1990s, we’d realized that things about documents could also be represented that way. And that we could build up symbolic documents to present things.

We’d long been wondering whether interactive user interfaces could also be unified into all of this.

And gradually we realized how to do this.

And after about 10 years of work, on May 1, 2007 we finally released a completely “reinvented” version of Mathematica that included this idea of “dynamic interactivity”.

You know, it’s been exciting watching the progress of Mathematica.

In a sense my idea with it was to use it automate as much as possible.

To take everything about computation that we humans don’t need to do, and to make it happen automatically.

Mathematica has all these algorithms inside. But the notion is that when we use it, we shouldn’t have to think about those.

We should just have to think about the problem we’re trying to solve, and Mathematica should automatically figure out what algorithms to use.

And should automatically figure out things like how to present a plot of the result, or how to set up a document or a user interface.

We want to automate as much as possible. And we want to have everything in the system as coherent and unified as possible.

Well, if you keep building and building with those principles, you steadily build up something pretty exciting.

And in these past few years we’ve really been having a blast.

We’ve had a pretty simple objective: let’s just implement everything.

All algorithms. All forms of computation.

And because of the automation and unification of the system, one gets a very interesting sort of recursive process.

Any one new piece of functionality can kind of “for free” make use of arbitrarily sophisticated stuff from elsewhere.

So it gets easier and easier to build.

Well, the result is this kind of plot of the number of functions in Mathematica as a function of time.

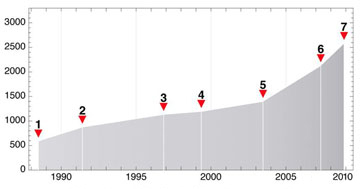
Perhaps because of its name, people think of Mathematica as being something about math.

Well, of course we pride ourselves on our achievements in automating mathematics.

But by now, math is a small part of what Mathematica does.

It used to be the case that we’d think about adding new functions to Mathematica.

Now we think about adding whole giant subsystems that each might be the complete work of several large independent software systems.

Well, so things with Mathematica were going really well.

We’d had a nice, profitable, private company, based here in Champaign, for many years.

We’d always been interested in sharing and communicating.

Even before the web we had a thing called MathSource, with all kinds of elaborate mechanisms for submitting and sharing material.

We had grand plans for communication by email, for getting documents by fax in response to automated phone calls, etc., etc.

Well, then the web came along.

And we started doing things with that.

In 1996 we put online The Integrator: a site for doing integrals.

And over the years, it’s done billions and billions of integrals.

With the numbers going up and down in different calculus seasons and so on.

In 1998 we put online MathWorld—a huge repository of mathematical information.

And in 2000 we launched our mathematical functions website, with more than 100,000 formulas on it.

Of course, really, our biggest knowledge base and knowledge repository was Mathematica itself.

For years and years we’d been pouring all those algorithms, and all that formal knowledge, into Mathematica.

And extending its language to be able to represent the concepts that were involved.

Well, while I’d been working on the NKS book, I’d kept on thinking: what will be the first killer app of this new kind of science?

When one goes out into the computational universe, one finds all these little programs that do these amazing things.

And it’s a little like doing technology with materials: where one goes out into the physical world and finds materials, and then realizes they’re useful for different things.

Well, it’s the same with those programs out in the computational universe.

There’s a program there that’s great for random sequence generation. Another one for compression. Another one for representing Boolean algebra. Another one for evaluating some kind of mathematical function.

And actually, over the years, more and more of the algorithms we add to Mathematica were actually not engineering step by step… but were instead found by searching the computational universe.

One day I expect that methodology will be the dominant one in engineering.

And that will be the real mega-killer industry of NKS.

But back in 2003, I was thinking about the first killer app for NKS.

And I started thinking back to my whole idea of computable knowledge. Of making the world’s knowledge computable.

We’d obviously achieved a lot in making formal knowledge computable with Mathematica.

But I wondered about all the other knowledge. Systematic knowledge. But knowledge about all these messy details of the world.

Well, I got to thinking: if we believe the paradigm and the discoveries of NKS, then all this complicated knowledge should somehow have simple rules associated with it.

It should somehow be possible to do a finite project that can capture it. That can make all that systematic knowledge computable.

Well, it was clear it wasn’t a small project.

And I still didn’t know if it was a doable project.

Of course, it helped that we had Mathematica.

Which is an incredibly productive language to be able to write things in. And a great practical platform for deploying things.

But still, there were many things that could wrong.

There could just be too much knowledge—too much data—in the world.

And it might not be possible to curate it in any reasonable way.

Or there might be too many different models and methods to implement.

With everything having to be separately built for every tiny subspecialty.

Or… another huge problem: maybe one could get all this knowledge into the system, but we humans wouldn’t be able to communicate with it.

With Mathematica, we could define a complete formal language for interacting with the system.

But when it comes to all systematic knowledge, it’s too big. People would never be able to learn a formal language.

Really the only way people can interact is using the language they all know: human natural language, English or whatever.

So we have to solve the problem of getting the system to understand that.

Well, of course, people have been trying to get computers to understand natural language for nearly 50 years, and it’s been notoriously difficult.

So that might have been another place our project would have been impossible.

I really didn’t know if the first decade of the 21^st century would be the time we could really first build a computational knowledge engine.

Or whether I was off by a decade, or five decades.

But still, around 2004 I decided it was worth a try.

We had Mathematica to actually build the thing. We had NKS as a paradigm for seeing what to do.

And we had a great company, with the resources to take on an impossible project like this.

And, perhaps even more importantly, with people who knew about all these different areas that would be needed in the project.

From building large-scale server systems, to creating linguistic algorithms, to the details of a zillion content specialties.

You see, we’d gradually been collecting at the company—both here in Champaign, and scattered around the world—a wonderful, eclectic collection of very talented people.

Who were used to working together, combining very different talents, on very diverse projects.

Well, the first thing that we did in thinking about our computable knowledge system was to work on data.

Could we take data on all sorts of things in the world, and curate it to the point where it was clean enough to compute with?

We started on things like countries and chemicals and things like polyhedra.

And we actually at first built what we call “data paclets” for Mathematica.

You see, in Mathematica you can compute the values of all sorts of mathematical functions and so on.

But we wanted to make it so there’d be a function that, say, computes the GDP of a country—by using our curated collection of data.

Well, we did lots of development of this, and in 2007, when we released our “reinvention” of Mathematica, it included lots of data paclets covering a variety of areas.

Well, that was great experience. And in doing it, we were really ramping up our data curation system.

Where we take in data from all sorts of sources, sometimes in real time, and clean it to the point where it’s reliably computable.

I know there are Library School people here today, so I’ll say: yes, good source identification really is absolutely crucial.

These days we have a giant network of data source providers that we interact with.

And actually almost none of our data now for example “comes from the web”.

It’s from primary sources.

But once we have the raw data, then what we’ve found is that we’ve only done about 5% of the work.

What comes next is organizing it. Figuring out all its conventions and units and definitions.

Figuring out how it connects to other data. Figuring out what algorithms and methods can be based on it.

And another thing we’ve found is that to get the right answer, there always has to be a domain expert involved.

Fortunately at our company we have experts in a remarkably wide range of areas.

And through Mathematica—and particularly its incredibly widespread use in front-line R&D—we have access to world experts in almost anything.

Who have been incredibly helpful to us.

Well, anyway, in 2007 we had released our first computable data—in Mathematica.

Meanwhile, we were busily constructing what would become Wolfram|Alpha.

In the past one might have thought that what we were doing would need having a whole artificial intelligence or something.

But in a sense we were cheating.

Like if we needed it to solve a physics problem, we weren’t going to have it reason its way through like a human would.

We were going to have it set up the equations, and then just blast through to the answer using the best modern mathematical physics.

In a sense the usual AI approach would have been to think like people imagined one had to in the Middle Ages: to figure everything out by logic.

But we were going to leverage the 300 or so years of development in science and so on, and just use the very best possible modern methods.

Of course, it helped that we had Mathematica, so that if we needed to solve a differential equation, or figure out some combinatorial optimization problem, that was, sort of, just free.

Well, so we set about just implementing all the systematic methods and models and so on from all areas of science, and beyond.

Pretty soon we’d racked up a million lines of Mathematica code—which is of course very, very concentrated compared to code in lower-level languages.

Then it was 2 million lines. Today it’s actually more than 8 million lines.

Implementing all those methods and models and so on.

Well, then what about the natural language understanding?

That might have just been plain impossible.

Perhaps what saved us is that the problem we have to solve is sort of the inverse of the problem people have spent so long on.

The usual problem is: here’s millions of actual English or whatever sentences. Go understand them.

Well, our problem is: there’s a certain—rather large—set of things we can compute about.

Now take a look at each human utterance that comes in. Then try to understand it, and see if we can compute from it.

Well, as it happens, I think we made some serious breakthroughs—pretty much on the basis of NKS ideas—that let us really do things there.

Taking the sort of undigested stream of thoughts that people, for example, type into an input field on our website. And having lots of little programs pick away at them, gradually understanding pieces.

Well, OK, so we can understand the question.

We’ve got data and methods to get answers. And we can compute.

But often we can compute lots and lots of different things.

So now the problem is to figure what to actually show as output.

Well, here we’d had a lot of experience in Mathematica with what we call “computational aesthetics”.

Of automating what to present and how to present it.

Well, putting all those things together, we gradually began to build Wolfram|Alpha.

Of course, then there were practical issues.

We’re not just going to the web to look things up.

We’re actually computing fresh new answers to every question as soon as it’s asked.

And that takes quite a bit of CPU power.

So we have to assemble a giant supercomputer-class cluster.

And hook it all up computing pieces of answers in parallel, and having webMathematica send back the results.

A big engineering project.

But one that came together that night 11 months ago today, 2 miles from here.

When we first let Wolfram|Alpha out into the world.

Well, it’s been exciting to see what’s happened.

It was a really difficult decision when to actually first release it.

We’d been adding so much—we knew the system would get better and better.

But there came a point where we couldn’t develop the linguistics—or even the content—without actually seeing how real people would interact with it.

And it’s been an interesting process of co-evolution. A little bit of evolution on the part of the people, about what to expect. And a lot of evolution on the part of the system, adapting to the foibles of all those humans out there using it.

We certainly haven’t created AI. But I think we’ve done something that’s not so far off from the science fiction of 50 years ago.

And in some respects, we’ve much exceeded what was expected.

Certainly in terms of the extent to which we can immediately democratize access to everything.

Through the web. Through mobile devices. And so on.

Our goal is to provide expert-level knowledge to anyone, anywhere, anytime.

It’s fun to compare what we’re doing to what you see in, say, that movie Desk Set from 1957, about the library-taking-over computer.

Or our friend HAL from 2001.

Now I suppose even though we were off by 12 years, we should have made a big effort to launch Wolfram|Alpha from Urbana rather than Champaign—just to give a bit of truth to the fictional birth of HAL.

But at least we were close.

Of course, as well as controlling a spacecraft, there’s a bunch HAL could do that Wolfram|Alpha can’t—at least yet.

So… what’s going to happen next?

Well, first of all, we continue to grind through more and more areas of knowledge.

It’s a never-ending project. But we’re getting faster, and we’re getting a long way.

We’re well past most of what’s in a typical reference library. We’re going into lots and lots of detail in lots of area.

Both in current data, and in lots of historical data.

But beyond adding existing knowledge, we want to start doing more things that are like what HAL might do: actually watching our environment.

Letting people, say, put an image feed into Wolfram|Alpha. Or upload data from their sensors.

And have Wolfram|Alpha use the knowledge it has, and the algorithms and methods it has, to do things with that.

Also, there’s NKS.

You see, in a sense, right now Wolfram|Alpha is a bit old-fashioned with respect to that.

It’s using science and so on that’s been developed in the past few hundred years.

But one of the points of NKS is that you can go onto into the computational universe, and in effect make new, creative discoveries automatically.

So that instead of just using existing methods and models and so on, Wolfram|Alpha can potentially discover new ones on the fly.

And be able not just to compute, but to invent on the fly.

Well, as I mentioned before, my experience has been that once one invents a paradigm, it takes a while to understand what’s possible within that paradigm.

It was that way with Mathematica, and with NKS. It’s that way with Wolfram|Alpha too.

But there’s more and more that’s coming out.

Wolfram|Alpha in a sense makes possible a new kind of computing: knowledge-based computing.

Where you’re not just starting from raw bits and algorithms, you’re starting from the knowledge of the world. And then building up computations.

Well, that changes the economics of lots of things, and makes it possible to insert computation in lots of places where it didn’t make sense before.

And right now, for example, we’re figuring out some amazing things about what happens when you combine the precise, systematic language of Mathematica with the broad freeform knowledge of Wolfram|Alpha.

It was in a sense very liberating with Wolfram|Alpha to take such a different approach to functionality and interface than in Mathematica.

They seemed in a sense quite incompatible. But now as we bring them together, we see that there is amazing strength in that diversity.

I guess I’ve spent most of my life now working on very large projects.

Mathematica. NKS. Now Wolfram|Alpha.

Each one has been gradually built, over a long period of time.

And I’ve worked very hard in each case to ensure that what we’re building is really solid, with all pieces in place.

Well, one consequence of that is that one builds lots of technology along the way. That has its own significance.

So, for example, from the way we built the interface to Mathematica, we’ve ended up now with another very interesting thing: computable documents. Which we’ll be releasing on a large scale later this year.

You know, I was thinking about Wolfram|Alpha, and about the long chain of circumstances that have led us to be able to build it.

I knew I’d been toying with things a bit like Wolfram|Alpha for a long time.

But I had my 50^th birthday last year. And for that I was looking at a bunch of archived material I have.

And I started looking at things I’d created when I was 12 years old.

And I realized something quite shocking.

There, with a typewriter and mapping pen, were collections of knowledge set up as best I could then.

A non-computer pre-Wolfram|Alpha.

Of course, I started typing in things from old stuff, and, yes, modern Wolfram|Alpha gets them right.

But I realized that in some sense I was probably fated for nearly 40 years to build a Wolfram|Alpha.

What’s really nice is that things came together to the point where we could actually do it.

So now we’re off and running with this giant project.

Well, I should wrap up here.

It’s great to be part of this celebration of 50 years of public computing in Illinois.

I’ll be very pleased if I’m lucky enough to be able to come to the 100-year version of this.

The projects that we’re doing still won’t be finished then.

Some of what will happen with them we can foresee. But some—as we build out these new paradigms—will be as seemingly unexpected as Wolfram|Alpha.

Until we look and can see the seeds already sowed today.

Thank you very much.